以下の記事で、\(\boldsymbol{\hat y} = X \boldsymbol w\)の最適解は、\(\boldsymbol w = ({}^t \!XX)^{-1}\boldsymbol {}^t \! X \boldsymbol y\)であることを紹介している。

重回帰分析を行うデータから重回帰式を算出してみた 以下の記事で読み込んだデータを元に、住宅価格の最適解を求めることを考える。 https://www.purin-it.com/...
今回は、上記計算式を利用して、重回帰式の算出を行うクラスを作成してみたので、そのサンプルプログラムを共有する。
\(\boldsymbol w = ({}^t \!XX)^{-1}\boldsymbol {}^t \! X \boldsymbol y\)を計算することで、重回帰式の最適解を算出するクラスの内容は、以下の通り。
import numpy as np
import pandas as pd
class OrigMultiRegressionLine:
# クラス変数
w = np.array([])
# 初期化処理
def __init__(self):
pass
# 与えられた入力データから、目的関数y=Xwのwを算出する
def fit(self, data_x, data_y):
# 入力データdata_xの先頭に、バイアス(1)を追加
x_df = pd.DataFrame(data_x)
x_df.insert(0, 'bias', 1)
# データをNumpy.ndarrayに変換し、計算に使うX,yを算出
X = x_df.values
y = data_y
# 目的関数y=Xwのwを算出
XtX = np.dot(X.T, X)
XtX_Inv = np.linalg.inv(XtX)
Xty = np.dot(X.T, y)
self.w = np.dot(XtX_Inv, Xty)
# 目的関数y=Xwのwを出力する
def printw(self):
# 小数点以下3桁まで+指数表記しない形式に設定後、wを出力
np.set_printoptions(precision=3, suppress=True)
print(self.w)
# 与えられた入力データxから、yの最適解を返却する
def predict(self, data_x):
return np.dot(self.w[1:], data_x) + self.w[0]また、上記OrigMultiRegressionLineクラスのfit・printwメソッドを呼び出して、目的関数\(\boldsymbol{\hat y} = X \boldsymbol w\)の\(\boldsymbol w\)を出力した結果は、以下の通り。
import numpy as np
from sklearn.datasets import fetch_california_housing
# カリフォルニアの住宅価格データセットを取得
housing = fetch_california_housing()
# 住宅価格データセットのデータをX, 結果をyとする
X = housing.data
y = housing.target
# OrigMultiRegressionLineクラスを使って、目的関数y=Xwのwを算出する
omr = OrigMultiRegressionLine()
omr.fit(X, y)
print("*** 目的関数y=Xwのwの値 ***")
omr.printw()

削除または保存していないWordドキュメントの復元方法【4DDiG Windowsデータ復元】ワード(Word)データ等のファイルを誤って削除してしまった場合は、通常はデータの復元ができませんが、4DDiGというソフトウェアを利用...
さらに、上記OrigMultiRegressionLineクラスのpredictメソッドを呼び出して、目的関数\(\boldsymbol{\hat y} = X \boldsymbol w\)の最適解\(\boldsymbol{\hat y}\)を出力した結果は、以下の通り。
import numpy as np
from sklearn.datasets import fetch_california_housing
# カリフォルニアの住宅価格データセットを取得
housing = fetch_california_housing()
# 住宅価格データセットのデータをX, 結果をyとする
X = housing.data
y = housing.target
# OrigMultiRegressionLineクラスを使って、目的関数y=Xwのwを算出する
omr = OrigMultiRegressionLine()
omr.fit(X, y)
print("*** 目的関数y=Xwのwの値 ***")
omr.printw()
print()
# 先頭3件のデータx_data, 結果y_data, 目的関数wから算出した結果y_hatを出力する
print("*** 目的関数y=Xwから算出した結果 ***")
for idx in range(3):
print(" *** x_data[{0}]の値 ***".format(idx))
x_data = X[idx]
print(x_data)
print(" *** y_data[{0}]の値 ***".format(idx))
y_data = y[idx]
print(y_data)
print(" *** y_hat[{0}]の値 ***".format(idx))
print(omr.predict(x_data))
print()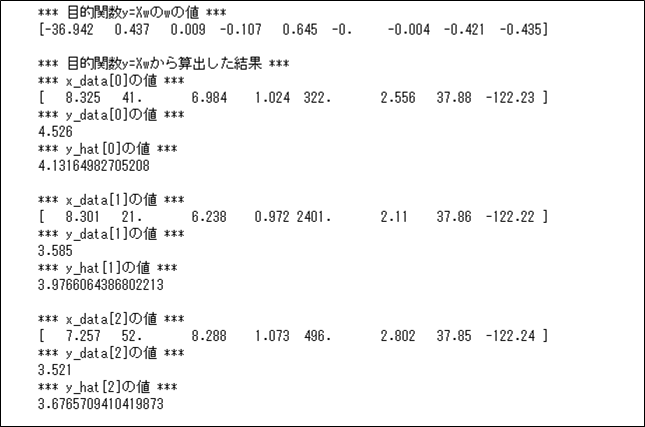
要点まとめ
- \(\boldsymbol{\hat y} = X \boldsymbol w\)の最適解は、\(\boldsymbol w = ({}^t \!XX)^{-1}\boldsymbol {}^t \! X \boldsymbol y\)であることを利用すると、重回帰式を算出できる。





