PythonにはJavaと同じ「オブジェクト指向」という概念があり、データと処理をまとめた「クラス」を定義し、その「クラス」から「インスタンス」を複数作成することができる。
今回は、以前このブログで紹介した回帰直線の算出を行うクラスを作成してみたので、そのサンプルプログラムを共有する。
なお、「クラス」についての詳細は、以下のサイトを参照のこと。
https://it-biz.online/python/class-2/
以下の記事の「回帰直線のa,bの計算」で実施している内容を、回帰直線を算出するクラスにまとめた結果は、以下の通り。

回帰直線を求める際にデータを標準化してみた このブログの以下の記事で、最小2乗法と最急降下法を用いて回帰直線を求めている。 https://www.purin-it.co...
import numpy as np
class OrigRegressionLine:
# クラス変数
eta = 0.001 # 学習率η
repeat_num = 10000 # 最急降下法の繰り返し回数
# 初期化処理
def __init__(self):
# 目的関数y=ax+bのa,bを求めるための初期値を宣言
# a,b(標準化後)を初期化
self.a_std = 1
self.b_std = 1
# a,b(標準化前)を初期化
self.a = 0
self.b = 0
# 与えられた入力データから、目的関数y=ax+bのa,b(標準化前)を算出する
def fit(self, data_x, data_y):
# 入力データを標準化する
input_data_x_std = self.__standardize(data_x)
input_data_y_std = self.__standardize(data_y)
# 最急降下法でa,b(標準化後)の値を算出
for num in range(OrigRegressionLine.repeat_num):
self.a_std = self.a_std - OrigRegressionLine.eta \
* self.__da_f(self.a_std, self.b_std, input_data_x_std, input_data_y_std)
self.b_std = self.b_std - OrigRegressionLine.eta \
* self.__db_f(self.a_std, self.b_std, input_data_x_std, input_data_y_std)
# 入力データの値(標準化前)の平均・標準偏差を算出
x_ave = data_x.mean()
x_stdd = data_x.std()
y_ave = data_y.mean()
y_stdd = data_y.std()
# 算出した直線(y = a_std * x + b_std)を標準化戻し後の、a,bの値を算出
self.a = self.a_std * y_stdd / x_stdd
self.b = -self.a_std * y_stdd * x_ave / x_stdd + self.b_std * y_stdd + y_ave
# 与えられたx座標から、y座標の予測値を返却する
def predict(self, data_x):
return self.a * data_x + self.b
# 入力データ(input_data)を標準化する
# メソッド名の先頭に__を付与することで、プライベートメソッドとする
def __standardize(self, input_data):
ave_val = input_data.mean()
std_val = input_data.std()
if std_val == 0:
return []
else:
return (input_data - ave_val) / std_val
# 最急降下法で利用するda_fを定義
def __da_f(self, a, b, input_data_x, input_data_y):
ret = 0
input_data_cnt = len(input_data_x)
for tmp in range(input_data_cnt):
tmp_x = input_data_x[tmp][0]
tmp_y = input_data_y[tmp][0]
ret = ret + (( a * tmp_x + b - tmp_y ) * tmp_x) / input_data_cnt
return ret
# 最急降下法で利用するdb_fを定義
def __db_f(self, a, b, input_data_x, input_data_y):
ret = 0
input_data_cnt = len(input_data_x)
for tmp in range(input_data_cnt):
tmp_x = input_data_x[tmp][0]
tmp_y = input_data_y[tmp][0]
ret = ret + ( a * tmp_x + b - tmp_y ) / input_data_cnt
return ret
また、上記OrigRegressionLineクラスのfitメソッドを呼び出してグラフ化した結果は、以下の通り。
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
# 入力データの読み込み
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341],
[35,360], [34,339], [32,329], [28,283], [35,372],
[33,342], [28,262], [32,328], [33,326], [35,354],
[30,294], [29,275], [32,336], [34,354], [35,368]])
# 入力データのx座標、y座標の抜き出し
input_data_x = input_data[:, 0]
input_data_y = input_data[:, 1]
# 入力データを訓練用とテスト用で分割
# test_sizeには、テストデータの割合を指定する
# random_stateを指定することで、分割方法を固定できる
train_data_x, test_data_x, train_data_y, test_data_y \
= train_test_split(input_data_x, input_data_y, test_size=0.2, random_state=0)
# OrigRegressionLineクラスを利用するため、抜き出したtrain_dataの
# x座標・y座標を、2次元1列の配列とする縦ベクトルに変更
train_data_x = train_data_x.reshape(-1, 1)
train_data_y = train_data_y.reshape(-1, 1)
# OrigRegressionLineクラスの回帰直線のa,bの値を算出
orl = OrigRegressionLine()
orl.fit(train_data_x, train_data_y)
print("*** a,bの値 ***")
print("a = " + str(orl.a) + ", b = " + str(orl.b))
# train_dataの値を散布図で表示
train_data_x = train_data_x.reshape(1, -1)
train_data_y = train_data_y.reshape(1, -1)
plt.scatter(input_data_x, input_data_y)
plt.title("train_data")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(26, 36)
plt.ylim(0, 450)
plt.grid()
# 算出した直線(y = ax + b)を追加で表示
x = np.linspace(26, 36, 1000)
y = orl.a * x + orl.b
plt.plot(x, y, label='y = ax+b', color='darkviolet')
plt.legend()
plt.show()
# test_dataの値を散布図で表示
test_data_x = test_data_x.reshape(1, -1)
test_data_y = test_data_y.reshape(1, -1)
plt.scatter(test_data_x, test_data_y)
plt.title("test_data")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(26, 36)
plt.ylim(0, 450)
plt.grid()
# 算出した直線(y = ax + b)を追加で表示
x = np.linspace(26, 36, 1000)
y = orl.a * x + orl.b
plt.plot(x, y, label='y = ax+b', color='darkviolet')
plt.legend()
plt.show()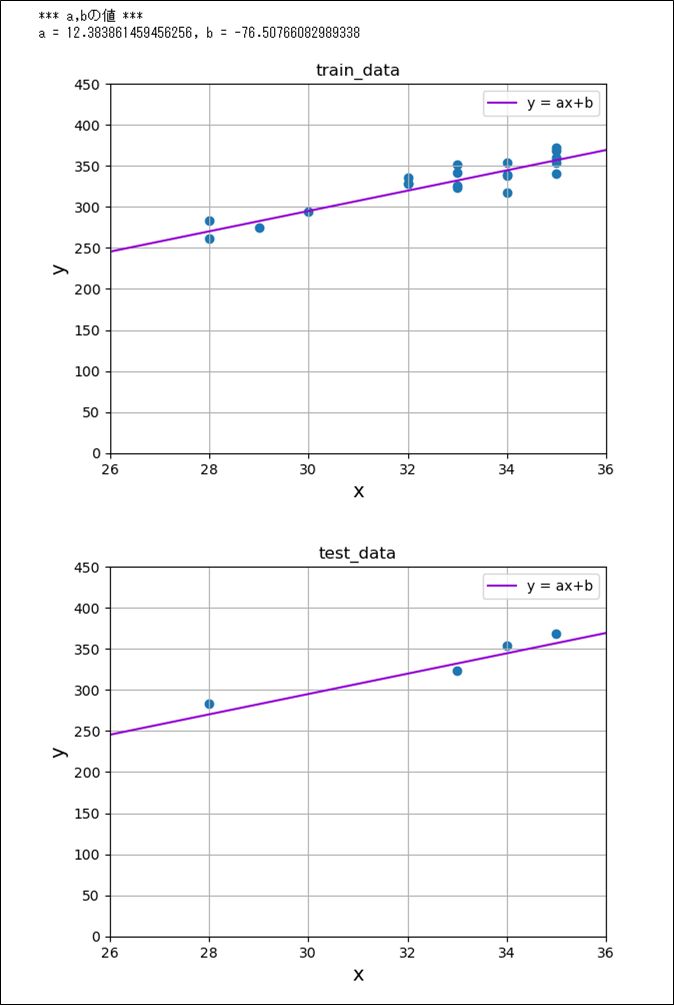
さらに、上記OrigRegressionLineクラスのfitメソッド/predictメソッドを呼び出して出力した結果は、以下の通り。
import numpy as np
from sklearn.model_selection import train_test_split
# 入力データの読み込み
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341],
[35,360], [34,339], [32,329], [28,283], [35,372],
[33,342], [28,262], [32,328], [33,326], [35,354],
[30,294], [29,275], [32,336], [34,354], [35,368]])
# 入力データのx座標、y座標の抜き出し
input_data_x = input_data[:, 0]
input_data_y = input_data[:, 1]
# 入力データを訓練用とテスト用で分割
# test_sizeには、テストデータの割合を指定する
# random_stateを指定することで、分割方法を固定できる
train_data_x, test_data_x, train_data_y, test_data_y \
= train_test_split(input_data_x, input_data_y, test_size=0.2, random_state=0)
# OrigRegressionLineクラスを利用するため、抜き出したtrain_data,test_dataの
# x座標・y座標を、2次元1列の配列とする縦ベクトルに変更
train_data_x = train_data_x.reshape(-1, 1)
train_data_y = train_data_y.reshape(-1, 1)
test_data_x = test_data_x.reshape(-1, 1)
test_data_y = test_data_y.reshape(-1, 1)
# OrigRegressionLineクラスの回帰直線のa,bの値を算出
orl = OrigRegressionLine()
orl.fit(train_data_x, train_data_y)
print("*** a,bの値 ***")
print("a = " + str(orl.a) + ", b = " + str(orl.b))
print()
# 算出した回帰直線から、test_dataのx座標からy座標の値を算出し、
# 実際のテストデータの値と比較
predict_data_y = orl.predict(test_data_x)
print("*** test_data_xの値 ***")
print(test_data_x.reshape(1, -1))
print("*** test_dataのx座標から算出したy座標の値 ***")
print(predict_data_y.reshape(1, -1))
print("*** test_data_yの値 ***")
print(test_data_y.reshape(1, -1))
要点まとめ
- PythonにはJavaと同じ「オブジェクト指向」という概念があり、データと処理をまとめた「クラス」を定義し、その「クラス」から「インスタンス」を複数作成することができる。





