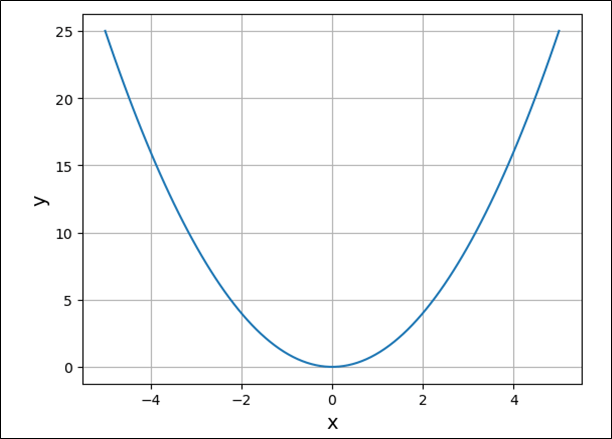
\(y=x^2\)の関数のグラフは以下の通りで、これを見ると\(x=0\)の場合に\(y\)が最小値(局値)を取ることが確認できるが、この\(y\)が最小となる\(x\)を求める方法の1つに「最急降下法」がある。
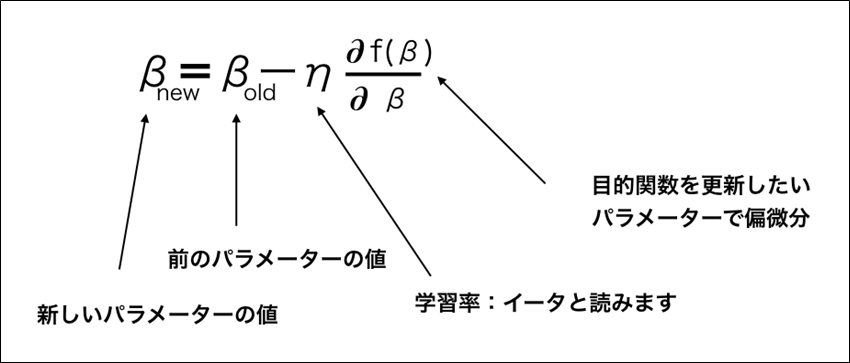
最急降下法は、接線の傾きを順次調べることによって、傾きが0になる\(x\)の値に近づけて行く方法で、以下の更新式を繰り返すことで、\(y\)が最小となる\(x\)を求めることができる。
今回は、最急降下法を用いて、二次関数の最小値(局値)の値を確認してみたので、そのサンプルプログラムを共有する。
前提条件
下記記事のAnacondaをインストールしJupyter Notebookを利用できること
\(y=x^2\)とその接線のグラフ
例えば、\(y=x^2\)の、\(x=4\)における接線は\(y=8x-16\)で計算され、その際のグラフを描くソースコードとグラフは、以下のようになる。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 | %matplotlib inline import numpy as np import matplotlib.pyplot as plt def f(x): return x**2 def d_f4(x): return 8 * x - 16 # -5～5までを100等分した値をxとする x = np.linspace(-5, 5, 100) # 上記xに対応するyの値(=xの2乗)を算出 y = f(x) # 上記関数の、x=4における接線 y_df4 = d_f4(x) # x,y,y_df4に対応する値を設定し、凡例を表示 plt.plot(x, y, label="y=x^2") plt.plot(x, y_df4, label="y=8x-16") plt.legend() # x軸・y軸のラベルを表示 plt.xlabel("x", size=14) plt.ylabel("y", size=14) # x軸・y軸の表示範囲を指定 plt.xlim(-1, 5) plt.ylim(0, 25) # グリッド線を表示 plt.grid() # x,yに対応する値のグラフを表示 plt.show() |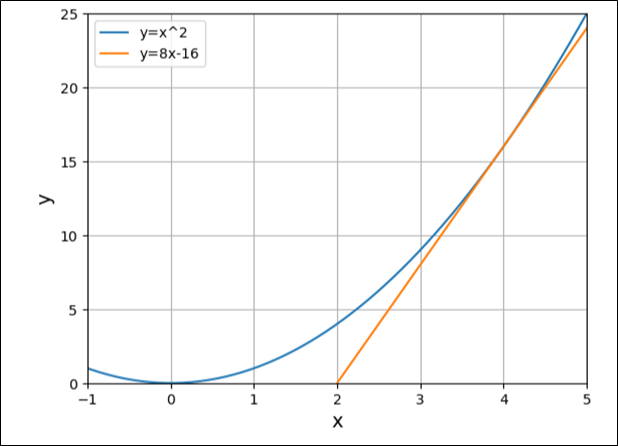
同様に、\(y=x^2\)の接線を、\(x=3\),\(x=2\),\(x=1\)と描いた結果は以下の通りで、だんだん傾きが0に近づくことが確認できる。
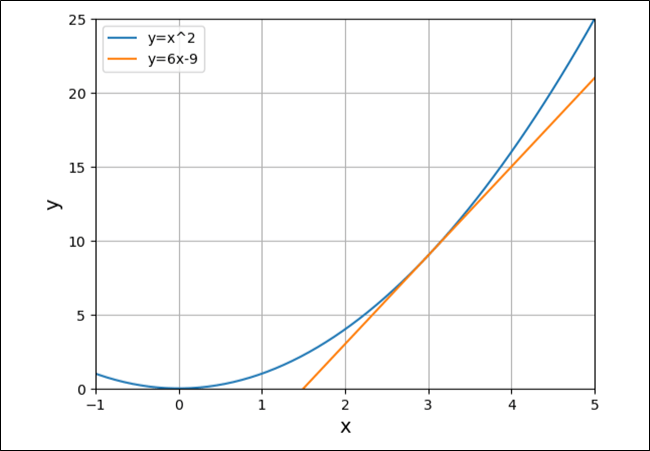
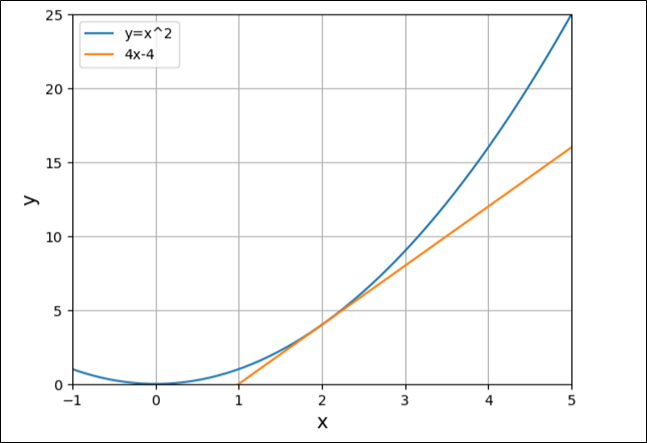
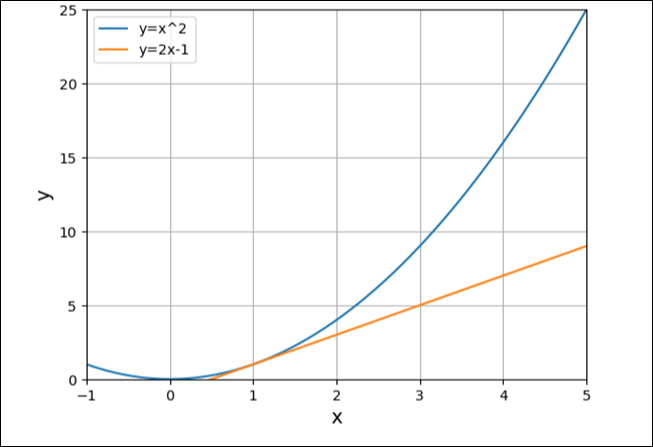
そして、\(x=0\)となると、以下のように、傾きが0になることが確認できる。
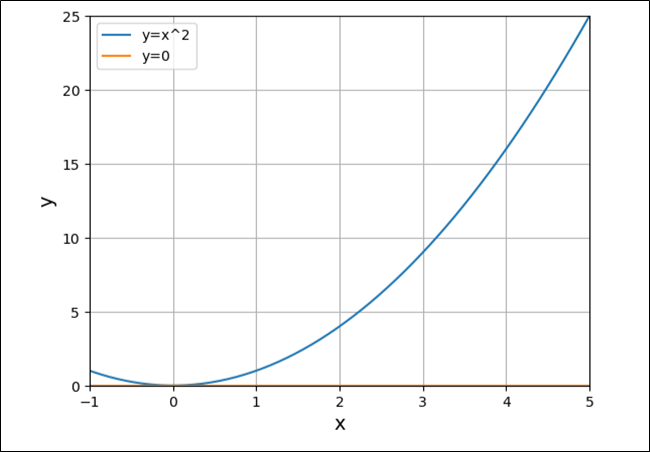
最急降下法を用いた二次関数の最小値(局値)の確認
実際に、最急降下法を用いて、\(x\)の値が\(0\)に近づくことを確認してみる。
なお、この記事の冒頭で紹介した通り、最急降下法で、以下の更新式を繰り返すことで、\(y\)が最小となる\(x\)を求めることができる。
\(y=x^2\)をxについて微分すると、\(y=2x\)となるので、最急降下法を用いた\(x\)の値の変化をいくつか確認した結果は、以下のようになる。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | def f(x): return x**2 def d_f(x): return 2*x # xの初期値 x = 4 print("x = " + str(x) + ", y = " + str(f(x))) # 学習率η eta = 0.1 # 更新式を10回分繰り返し、xの値が0に近づくことを確認 for num in range(10): x = x - eta * d_f(x) print("x = " + str(x) + ", y = " + str(f(x)) + ", d_fx = " + str(d_f(x))) |
これを見ると、\(x\)の値がだんだん0に近づいていることが確認できる。なお、学習率ηは、結果を見て適当な値を設定している。
次に、最急降下法の、更新式の繰り返し回数を200回・1,000回にした結果は、以下の通り。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | def f(x): return x**2 def d_f(x): return 2*x # xの初期値 x = 4 # 学習率η eta = 0.01 # 更新式を200回分繰り返した場合を確認 for num in range(200): x = x - eta * d_f(x) # x,y,df(x)の最終値を確認 y = f(x) d_f = d_f(x) print("x = " + str(x) + ", y = " + str(y) + ", d_fx = " + str(d_f)) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | def f(x): return x**2 def d_f(x): return 2*x # xの初期値 x = 4 # 学習率η eta = 0.01 # 更新式を1,000回分繰り返した場合を確認 for num in range(1000): x = x - eta * d_f(x) # x,y,df(x)の最終値を確認 y = f(x) d_f = d_f(x) print("x = " + str(x) + ", y = " + str(y) + ", d_fx = " + str(d_f)) |
最急降下法の、更新式の繰り返し回数を1,000回にした最終結果の数値を、散布図で表現した結果は以下の通りで、これを見ると確かに\(x=0\)に近づいているのが確認できる。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | %matplotlib inline import matplotlib.pyplot as plt def f(x): return x**2 def d_f(x): return 2*x # xの初期値 x = 4 # 学習率η eta = 0.01 # 最急降下法を1,000回分繰り返した場合を確認 for num in range(1000): x = x - eta * d_f(x) # x,y,df(x)の最終値を確認 y = f(x) d_f = d_f(x) print("x = " + str(x) + ", y = " + str(y) + ", d_fx = " + str(d_f)) # x,yの最終値を散布図で確認 plt.scatter(x, y) plt.title("x&y last value") plt.xlabel("x", size=14) plt.ylabel("y", size=14) plt.xlim(-0.1, 0.1) plt.ylim(-0.1, 0.1) plt.grid() plt.show() |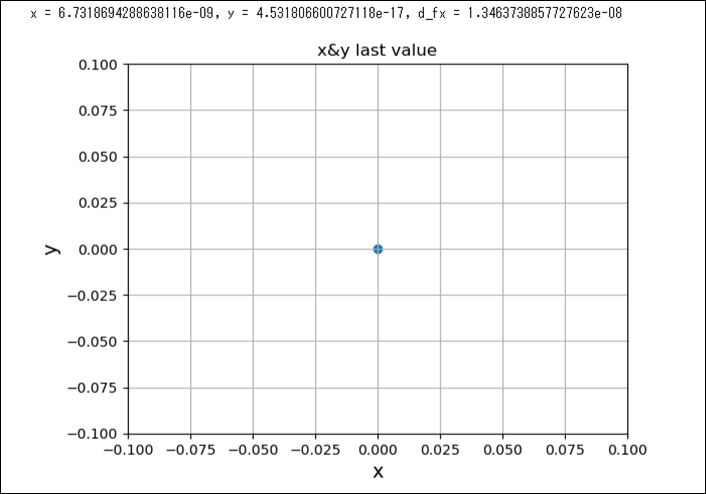
また、最急降下法の、更新式を1,000回繰り返した際の、xの値の変化は以下の通りで、約300回の繰り返しで\(x=0\)に近づいているのが確認できる。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | %matplotlib inline import matplotlib.pyplot as plt def f(x): return x**2 def d_f(x): return 2*x # xの初期値 x = 4 # 学習率η eta = 0.01 # xの値の変化を格納 repeat_num = [] x_value = [] # 最急降下法を1,000回分繰り返した場合を確認 for num in range(1000): x = x - eta * d_f(x) repeat_num.append(num) x_value.append(x) # x,y,df(x)の最終値を確認 y = f(x) d_f = d_f(x) print("x = " + str(x) + ", y = " + str(y) + ", d_fx = " + str(d_f)) # xの値の変化(repeat_num,x_value)の値の変化をグラフ化 plt.plot(repeat_num, x_value) plt.title("x value change") plt.xlabel("repeat_num", size=14) plt.ylabel("x_value", size=14) plt.grid() plt.show() |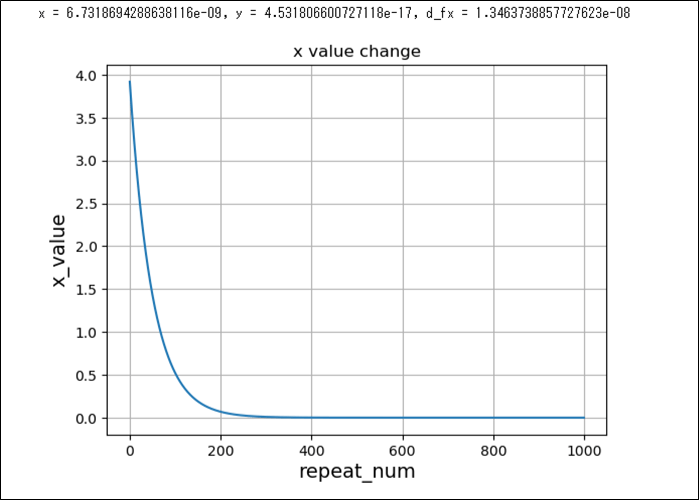
要点まとめ
- 最急降下法は、接線の傾きを順次調べることによって、傾きが0になる値に近づけて行く方法で、これを用いて二次関数の局値を求めることができる。
